偏差値とは?仕組みと活用法を解説
高校受験や学校選びをする際に、「偏差値」という言葉をよく耳にします。 「今回の模試では偏差値60だった」「○○高校の偏差値は60くらい」といった使われ方が一般的です。
当サイトにも、「模試で300点満点中○○点でした。偏差値はどのくらいになりますか?」といったご質問をいただくことがあります。 また、「偏差値の求め方」や「500点満点250点 偏差値」などの検索キーワードで訪れる方も少なくありません。 それだけ偏差値は、受験生や保護者にとって重要な指標だと言えるでしょう。
ただし、偏差値について、まず押さえておきたいのは「個々の得点だけでは偏差値を計算できない」という点です。 偏差値を求めるには、その試験を受けたすべての生徒の得点データが必要です。
偏差値とは統計学に基づいた指標であり、その計算方法は意外と知られていません。 そこで今回は、偏差値の仕組みや活用法について、分かりやすく解説していきます。
学校の定期テストでは、平均点は公開されることが多いものの、偏差値まで公表されることはほとんどありません。 確かに平均点が分かれば、自分の得点との差(偏差)を把握することはできます。 しかし、それだけでは、自分が全体の中でどの位置にいるのかを正確に知ることはできません。
例えば、平均点が60点のテストで50点を取った場合を考えてみましょう。 平均点との差(偏差)は「-10点」ですが、テストの点数のばらつきによって、自分の位置が大きく異なる場合があります。
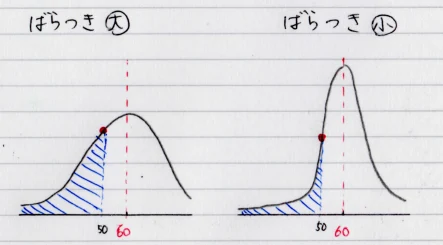
ばらつきが大きい場合:下位40%に位置する可能性がある
ばらつきが小さい場合:下位20%に位置する可能性がある
このように、平均点だけでは全体の中での自分の位置を正確に把握することが難しいのです。
そこで役立つのが偏差値という指標です。偏差値は、自分の得点が全体の中でどの位置にあるかを分かりやすく数値化したものです。
偏差値では、「50」が全体の平均点に相当します。そこから、以下のように全体の分布を大まかに位置づけることができます。 (全受験者の成績を表すヒストグラムが正規分布とすると)
偏差値70以上、または30以下:全体の上位2%、または下位2%
偏差値60以上、または40以下:全体の上位16%、または下位16%
偏差値50:全体のちょうど真ん中(平均)
このように偏差値を活用すれば、自分の得点が全体のどの辺りに位置しているのかをイメージしやすくなります。学校選びや進路を考える際にも、大いに役立つ指標と言えるでしょう。
偏差値は、単に得点の高低だけでなく、自分の学力を全体の中で相対的に把握するための便利な指標です。 ただし、得点だけで求めることはできないため、模試などの正式な結果を参考にしましょう。
また、偏差値はあくまで一つの目安であり、最終的には「自分の目標や適性に合った学校を選ぶ」ことが最も重要です。 偏差値だけにとらわれず、志望校や学習計画をじっくり考えることをお勧めします。
(2014.11.09更新)

